Уравнение затухающих колебаний

Затухание колебаний

Свободные колебания в реальных условиях не могут продолжаться вечно. Для механических систем всегда имеет место сопротивление среды, вследствие чего энергия движения объекта рассеивается при трении. В электромагнитных контурах колебания затухают за счет сопротивления проводников.

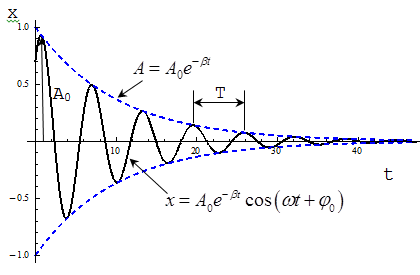
График затухающих колебаний

Уравнение затухающих колебаний

Уравнение затухающих колебаний описывает движение реальных колебательных систем. В дифференциальной форме оно записывается следующим образом:

  \[\frac{\partial^2 x}{\partial t^2} +2\beta \frac{\partial x}{\partial t} +\omega_0^2 x=0\]

Из этого выражения можно получить еще одну каноническую форму:

  \[x=Ae^{-\beta t} \cos (\omega t +\varphi_0 )\]

либо x=Ae^{-\beta t} \sin (\omega t +\varphi_0 ).

Здесь x и t – координаты пространства и времени, А – первоначальная амплитуда. \beta – коэффициент затухания, который зависит от сопротивления среды r и массы колеблющегося объекта m:

  \[\beta = \frac{r}{2m} \]

Чем больше сопротивление среды, тем больше энергии рассеивается при вязком трении. И наоборот – чем больше масса (а значит, инерционность) тела, тем дольше оно будет продолжать движение.

Циклическая частота свободных колебаний (такой же системы, но без трения) \omega_0 учитывает силу упругости в системе (например, жесткость пружины k):

  \[\omega_0 =\frac{k}{m} \]

Строго говоря, в случае затухающих колебаний нельзя говорить про период – время между повторяющимися движениями системы постоянно увеличивается. Однако если колебания затухают медленно, для них с достаточной точностью можно определить период Т:

  \[T=\frac{2\pi}{\sqrt{\omega_0^2 -\beta^2}} \]

Циклическая частота затухающих колебаний

Еще одна характеристика затухающих колебаний – циклическая частота:

  \[\omega =\sqrt{\omega_0^2 -\beta^2} \]

Время релаксации – это коэффициент, показывающий, за какое время амплитуда колебаний уменьшится в е раз:

  \[\tau = \frac{1}{\beta} \]

Отношение амплитуды изменяющейся величины в двух последовательных периодах называют декрементом затухания:

  \[D= \frac{A(t)}{A(t+T)} =e^{\beta T} \]

Эту же характеристику при расчетах часто представляют в виде логарифма:

  \[\lambda =lnD=\beta T\]

Добротность Q характеризует, насколько силы упругости системы превышают силы сопротивления среды, препятствуя диссипации энергии:

  \[Q= \frac{\sqrt{mk}}{r} \]

Примеры решения задач

ПРИМЕР 1

Задание После того, как к пружине подвесили груз, она растянулась на 9,8 см. Пружина колеблется в вертикальном направлении, \lambda = 3,1 . Определить период колебаний.
Решение Так как пружина растягивается под весом, то на нее действует сила тяжести:

  \[F=mg \]

Силе тяжести противодействует сила упругости пружины:

  \[F=k\Delta x\]

Из двух выражений найдём коэффициент упругости:

  \[k= \frac{mg}{\Delta x} \]

Подставим коэффициент упругости в формулу для периода затухающих колебаний:

  \[T=\frac{2\pi}{\sqrt{\omega_0^2 -\beta^2}} =\frac{2\pi}{\sqrt{\left(\frac{k}{m} \right)^2 -\beta^2}} \frac{2\pi}{\sqrt{\left(\frac{g}{\Delta x} \right)^2 -\beta^2}} \]

Зная, что логарифмический декремент затухания \lambda =\beta T, выразим из него неизвестную величину \beta, подставим в знаменатель формулы и выразим Т:

  \[ T=\sqrt{\frac{(\lambda^2 +4\pi^2 )\Delta x}{g}} =\sqrt{\frac{(3,1^2 +4\pi^2 )\cdot 0,098}{9,8}} =0,7 c \]
Ответ T = 0,7 c